Rubiks Encryption

I'm bored, I like Rubik's cubes, and I enjoy cryptography. So let's make something interesting and combine the lot. Have you ever wanted to hand someone a scrambled Rubik's cube, with everything from the randomness of the scramble to the placement of your hands passing along an encrypted message? Well, neither have I! But here's a method of doing so anyway.
Concept Overview
The core idea revolves around mapping alphanumeric characters to specific numerical products, then represented by pairs of colors on the cube. Each face of the cube is designated a number, which can be selected arbitrarily at the time of encryption, as long as the scheme has also been passed along to the party decrying the cube. By scrambling the cube in such a way that certain colors land in certain positions, you're able to encode a message that can be (fairly) easily decrypted with a bit of math and a reference sheet.
Color-to-Number Mapping
For a number set to work off of, I decided to run with {1, 2, 3, 5, 7, 8}. This set allows for 21 possible sums, with a max of 64 (a nice number if I do say so myself). Unfortunately, I couldn't find a set that created more sums, but to be blunt there wasn't much of a search for one.
Each number in this set can be arbitrarily applied to the colors of any order cube. For the purposes of this article, we will be discussing a standard 3x3 cube with the following designations:
- White (Top): 1
- Green (Left): 5
- Blue (Right): 2
- Red (Front): 3
- Orange (Back): 8
- Yellow (Bottom): 7
This assignment ensures that each color is associated with a unique prime or composite number, facilitating the encoding process.
Character Encoding Scheme
Given the constraints of the set we chose, we can only map 21 alphanumeric characters. And so numbers will be excluded, as well as letters that can be substituted with phonetic equivalents (ex. "C" is substituted with "S" or "K" as needed) or easily obtainable alternatives.
Again, this lexicon just like the set utilized can be adapted arbitrarily to suit the needs of the encryption, given the decrypting party is aware of the changes. Products can be the sums of multiple variants of our given set, which will aid in upcoming segments pertaining to cubie constraints.
| Product | Character |
|---|---|
| 1 | A |
| 2 | B |
| 3 | D |
| 4 | E |
| 5 | F |
| 6 | G |
| 7 | H |
| 8 | I |
| 9 | J |
| 10 | K |
| 14 | L |
| 15 | M |
| 16 | N |
| 21 | O |
| 24 | P |
| 25 | R |
| 35 | S |
| 40 | T |
| 49 | U |
| 56 | W |
| 64 | Y |
Encoding Process
To encode a message:
Convert Characters to Products: Translate each character in the message to its corresponding numerical product using the lexicon.
Determine Color Pairs: For each product, identify a pair of numbers from the set {1, 2, 3, 5, 7, 8} that multiply to the product. Again, these numbers correspond to specific colors on the cube.
- Determine Encryption Salt: This is an added security layer to the encryption, as well as the only way messages can be decoded from a scrambled cube. For a salt, we'll be utilizing the orientation of the cube at the time of the scramble. The easiest way to remember this will be the top center color, and front center color.
Assign Colors to Cubies: Place the color pairs on adjacent cubies of the Rubik's Cube, adhering to the cube's color adjacency constraints. This is likely the hardest part of the encoding process, as it may require refining the color pairs utilized or altering the message as a whole.
- Solve The Cube: I'm not here to teach you this. If you're reading this article, you either know how, or can learn from teachers much better than me. My teaching ability has been described as "a pain in the ass" and "you suck I'll do it myself". Solve the cube into the previously calculated positions from step 4.
Record Cube Configuration: Document the cube's configuration after encoding the entire message, as this serves as the encrypted form. Or just yeet it at whoever you want to decode it, that should work fine.
Decoding Process
To decode the message:
Determine The Salt: Get the initial orientation of the cube pre-scramble. Waterboarding is an effective method, but politely asking or simply remembering may very well work.
- Convert Colors to Numbers: Utilizing the previously waterboarded information, memory, or an act of kindness, convert the colors into their numerical equivalents.
- Read Color Pairs: Beginning at the front face of the cube, at the top left cubie, begin reading the color pairs in a clockwise fashion. For each pair, multiple the two numbers together and log their sum.
Map Products to Characters: Finally, for each product you devised in step 2, log its corresponding character from the lexicon. And BAM! You have a decoded message, probably relating to some spy shit or an edgy message about cats.
Practical Considerations
Color Adjacency Constraints: Because cubes are creatures of the third dimension, we are limited to the number of colors available to us (and their placement, assuming you've never taken a hammer to your cube). For example, when an encryption requires the right side edge to be a blue piece. The blue face only contains four blue edges, each with corresponding colors: blue/yellow, blue/orange, blue/red, and blue/white. This means we're limited to which block can be placed in that position, depending on the characters required for the adjacent face.
- Message Length and Cube Faces: Short messages of four characters or less are easily encoded on a single face, but anything greater will require multiple faces and the complexities that brings. This makes it essential to plan ahead, and often backtrack, in order to decide the specific cubie placement across the cube (and can, at points, become impossible with some messages). Utilizing higher order cubes can mitigate this issue, or at least shove it in the corner for a while.
Substitution for Unrepresented Characters: With the limiteed number of products given with out chosen set, not all characters can be represented. As such, substitions are required. These can be again substituted for each use-case, but I feel I did a good job and would be very unhappy to find out you did such a heretical thing. Digits also don't fit, so enjoy spelling out nHentai codes.
Example 1: Encoding "NYAMEOW"
Let's encode the message "NYAMEOW" using the described method:
Convert Characters to Products:
- N = 16
- Y = 64
- A = 1
- M = 15
- E = 4
- O = 21
- W = 56
Determine Color Pairs:
- 16 = Blue × Orange
- 64 = Orange × Orange
- 1 = White × White
- 15 = Red × Green
- 4 = 2 × 5 → Blue × Blue
- 21 = 3 × 7 → Red × Yellow
- 56 = 7 × 8 → Yellow × Orange
Assign Colors to Cubies:
- Front Face (Red):
- N: Top-left (Blue), Top-center (Orange)
- Y: Top-right (Orange), Middle-right (Orange)
- A: Bottom-right (White), Bottom-center (White)
- M: Bottom-left (Red), Middle-left (Green)
- Right Face (Blue):
- E: Top-left (Blue), Top-center (Blue)
- O: Top-right (Red), Middle-right (Yellow)
- W: Bottom-right (Orange), Bottom-center (Yellow)
- Front Face (Red):
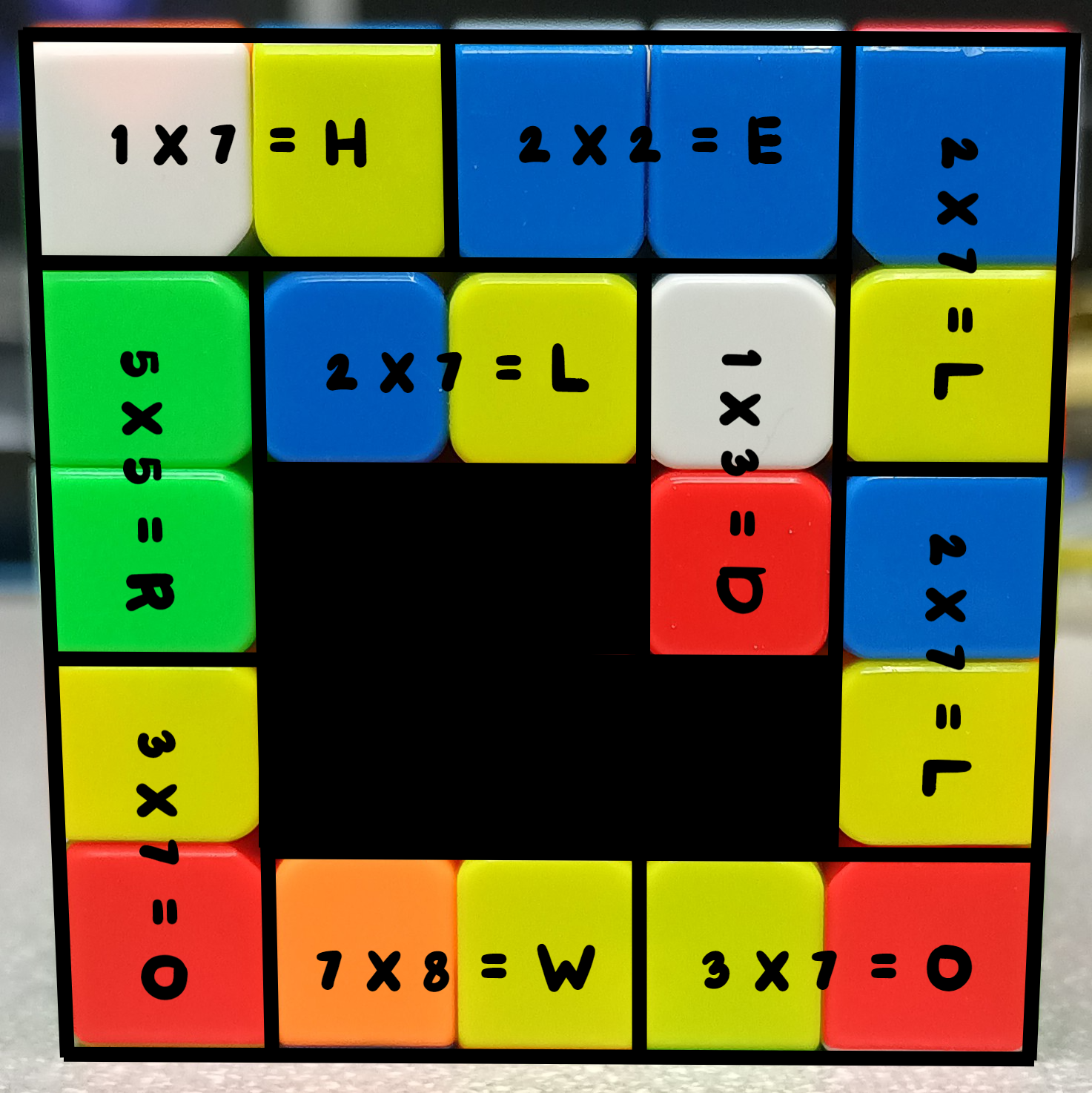
Example 2: Encoding "HELLOWORLD" on a higher-order cube
Convert Characters to Products:
- H = 7
- E = 4
- L = 14
- L = 14
- O = 21
- W = 56
- O = 21
- R = 25
- L = 14
- D = 3
Determine Color Pairs:
- 7 = 1 × 7 → White × Yellow
- 4 = 2 × 2 → Blue × Blue
- 14 = 2 × 7 → Blue × Yellow
- 14 = 2 × 7 → Blue × Yellow
- 21 = 3 × 7 → Red × Yellow
- 56 = 7 × 8 → Yellow × Orange
- 21 = 3 × 7 → Red × Yellow
- 25 = 5 × 5 → Green × Green
- 14 = 2 × 7 → Blue × Yellow
- 3 = 1 × 3 → White × Red
Assign Colors to Cubies:
- Front Face (Red):
- H: Top-left (White), Top-middle-left (Yellow)
- E: Top-middle (Blue), Top-middle-right (Blue)
- L: Top-right (Blue), Right-middle-top (Yellow)
- L: Right-middle (Blue), Right-middle-bottom (Yellow)
- O: Right-bottom (Red), Bottom-middle-right (Yellow)
- W: Bottom-middle (Yellow), Bottom-middle-left (Orange)
- O: Bottom-left (Red), Left-middle-bottom (Yellow)
- R: Left-middle (Green), Left-middle-top (Green)
- L: Center-top-left (Blue), Center-top-middle (Yellow)
- D: Center-top-right (White), Center-middle-right (Red)
- Front Face (Red):
You've now been cursed with this knowledge, congrats.